[Архив!] Чистая математика, физика, химия и т.п.: задачки для тренировки мозгов, никак не связанные с торговлей - страница 313

1,2,4,8,16,32 — единственный ответ

Доказательство, ihor?

Если вес какой то гири будет меньше 2^n, то суммарный вес будет меньше 63,

если больше то в последовательности весов которые можно получить этими гирями будут пробелы.

Логично. Вот решение:

Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.

Следующая (10-й):

Насчет минимальной гири 1 — не уверен

может две гири 2 и 3 тоже подойдут.

Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.

Гигант.
А программу выложишь? Просим, просим!

Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.

Насчёт 1 я был неправ.

В программе ничего интересного, простой перебор.

#include <stdio.h>

#define COUNT 63

bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=false;

// 1 — на одной чаше, 0 — гиря не участвует -1 — на второй чаше

for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if (ves > COUNT) return false;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) return false;

return true;
}

main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if (isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}

Доказательство без особых строгостей, но корректное.
Введем обозначения координат вершин, как показано на рисунке. Чтобы синее было квадратом, должно выполняться

x1-x2=y1-y4 ;
y1-y2=x1-x2;

а также

x3-x4=y2-y3;
y4-y3=x2-x3.

Из первых двух уравнений, если вспомнить уравнение графика, получим

x4-x2=A(sinx2-sinx4),

из третьего и четвертого

x3-x1=A(sinx1-sinx3).

Поскольку никаких ограничений на квадраты, кроме минимального их количества, не наложено, будем рассматривать только те случаи, когда квадраты симметричны относительно начала координат. Но тогда x4=-x2, x3=-x1 и то же самое с синусами. Наши уравнения приобретут вид:

sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A

Вспомним, какой график имеют функции от x2 и x1, стоящие в левых частях. Для этого посмотрим на рисунок: график имеет убывающие экстремумы как при положительных, так и при отрицательных x. Очевидно, что постепенно уменьшая число A, сможем получить такое количество корней, какое нам требуется, в том числе и 1978, и больше.

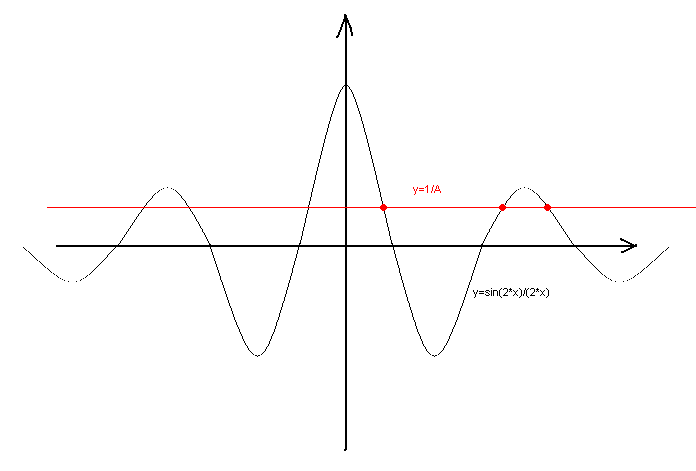
Полученные корни различные, причем относятся друг к другу сугубо иррационально. Думаю, не нужно доказывать подробно, что квадраты в этом случае попарно не равны.