Тестовая многопеременная многоэкстремальная функция.

В качестве идеи. Можно взять обычный ряд Фурье и считать, что каждое слагаемое вида cos(kwt) имеет свой собственный аргумент t. То есть частоты будут как монохроматический ряд, а время у каждого свое. Сколько слагаемых, столько и переменных. А уж экстремумов у этой дряни будет вообще немеряно. :-)

Можно даже коэффициент k выбросить. Все равно все слагаемые будут линейно независимы.

Ух! Хорошая идея. А можно пример какой нибудь? Правда... подозреваю, получатся волны, а значит все экстремумы min и мах будут одинаковыми, а это не спортивно.

Не силен в Фурье, поправьте меня, если требуется.

Пример:

F(x1,x2,x3,...,xn) = A1*cos(1*w*x1) + A2*cos(2*w*x2) + A3*cos(3*w*x3) + ... + An*cos(n*w*xn);

Константы A1,A2,A3, ... нужно выбирать разными, тогда и экстремумы будут разными. Варьируя w можно управлять плотностью экстремумов на единицу общема гиперкуба области определения функции F(). Лучше всего взять три переменных и поэкспериментировать. Расположение экстремумов и их величину даже можно визуально отобразить в кубической области.

Вы ведь хотите сложный случай, а усложнять всегда легче, чем упрощать. :-)))

Кстати, для того, чтобы экстремумы не накладывались друг на друга (а для предложенной функции часть экстремумов накладывается), можно 1. использовать кроме косинуса еще и синус и 2. (более важно) ввести еще сдвиг по фазе свой для каждого из слагаемых. он вполне может быть случайным.

Тогда общий вид аргумента для косинуса будет таким (n*w*xn + cn), где w и cn - константы.

Спасибо!

Примерно через неделю после моего последнего поста додумался до более изящного и простого, а главное - практичного решения. А вчера вспомнил про эту тему и решил поделится.

Можно представить тестовую функцию F как сумму n-го количества (чем сложнее хотим, тем больше берем) простых функций f(x,y) так:
F=f(x1,y1)+f(x2,y2)+f(x3,y3)+...++f(xn,yn)

Понятно что максимум/минимум F будет при x1=x2=x3....=xn и y1=y2=y3....=yn и решение будет выглядеть например так : (2,3,2,3,2,3,2,3,.....2,3). Но о том, что парные переменные равны в точке максимума/минимума знаем только мы, а алгоритм оптимизации - нет.

Пример.

Dream of the climber

(-15..15)
MAX(3.1415....;0.0)=15.284... одна точка
MIN()=0.0 множество точек

MathPow(MathSin(MathSqrt(MathAbs(x1 - 1.3) + MathAbs(y2))) + MathCos(MathSqrt(MathAbs(MathSin(x1))) + MathSqrt(MathAbs(MathSin(y2)))), 4.0)

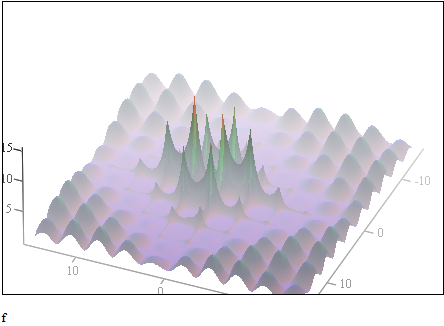
и соответственно для функции с n количеством парных переменных:

   
   cnt=1;
   while (cnt<=n)
   {
      sum+=pow(sin(sqrt(fabs(x1 - 0.13e1) + (double) fabs(x2))) + cos(sqrt(fabs(sin(x1))) + sqrt(fabs(sin((double) x2)))), 0.4e1);
      cnt++;
   }

И вообще, учитывая то, что почти все задачи так или иначе связанные с финансами являются оптимизационными, кажется странным, что никто кроме Yurixx не проявил интереса. Либо используют стандартные средства оптимизации тестера, либо не афишируют свои разработки.

В любом случае, попробуйте предложенную функцию со своим алгоритмом оптимизации что бы проверить насколько он хорош. Обычно такие функции, не дифференцируемые в точке экстремума трудны для оптимизации.

Буду рад увидеть здесь другие интересные, "трудные", и просто красивы функции.

Мне приходилось проявлять интерес, даже как-то выкладывал свою реализацию ГА на C++. Правда, в отличие от вас, я не вижу смысла придумывать столь сложные функции для тестирования, а предпочитаю тестировать на реальных данных. В качестве простейшего теста на работоспособность брал поиск коэффициентов полинома, аппроксимирующего некоторый набор точек по МНК.

1) Как мне представляется, что бы убедится, что алгоритм не "даст дуба" не реальных задачах, как раз и стоит прогнать на подобных "сложных" функциях, что бы иметь представление о сильных и слабых сторонах алгоритма.

2) "Гладкие" функции не представляют сложности ни для каких алгоритмов оптимизации. А откуда мы можем знать, какие "сюрпризы" таит в себе рынок? :)

Я тут только мимо проходил ;-), но вот мои 5 копеек.
ИМХО, изначальный посыл вообще неверный: т.е. нужно стремиться, чтобы оптимизируемая функция была максимально (по возможности, конечно) гладкой. Ведь на реальном рынке форма этой функции будет нестабильна, и малейшие отклонения не должны вызывать заметных изменений. Иначе даже при наличии хорошего алгоритма оптимизации - грош цена полученным оптимизированным параметрам в силу их заточенности на узкие экстремумы.

Не в ту степь.

Вы говорите про наборы параметров, которые будут "работать" в подавляющем большинстве случаев, имея ввиду, по видимому, про тестер стратегий в МТ.

Моя цель же была совершенно в другом - найти тестовую функцию содержащую иголку (типа в стоге сена) и содержащую разнообразный, так сказать, ландшафт. Чем быстрее алгоритм её найдет (за наименьшее количество запусков тестовой ф-ии), тем лучше алгоритм будет справляться с реальными задачами. Мои реальные задачи - обучение нейронных сетей и комитетов сетей, где возможны не только недифференцируемые точки, но и разрывы в экстремумах оптимизируемой функции.